

The goal of vital is to allow analysis of demographic data using tidy tools.
You can install the stable version from CRAN:
pak::pak("vital")You can install the development version from Github:
pak::pak("robjhyndman/vital")First load the necessary packages.
library(vital)
library(tsibble)
library(dplyr)
library(ggplot2)The basic data object is a vital, which is time-indexed
tibble that contains vital statistics such as births, deaths, population
counts, and mortality and fertility rates.
Here is an example of a vital object containing
mortality data for Norway.
norway_mortality <- norway_mortality |>
collapse_ages(max_age = 100)We can use functions to see which variables are index, key or vital:
index_var(norway_mortality)
#> [1] "Year"
key_vars(norway_mortality)
#> [1] "Age" "Sex"
vital_vars(norway_mortality)
#> age sex deaths population
#> "Age" "Sex" "Deaths" "Population"norway_mortality |>
filter(Sex != "Total", Year < 1980, Age < 90) |>
autoplot(Mortality) + scale_y_log10()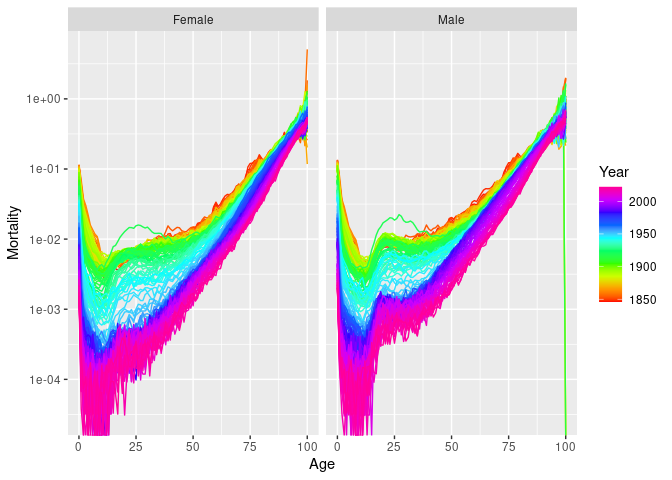
# Life table for Norwegian males in 2000
norway_mortality |>
filter(Sex == "Male", Year == 2000) |>
life_table()
#> # A vital: 101 x 13 [?]
#> # Key: Age x Sex [101 x 1]
#> Year Age Sex mx qx lx dx Lx Tx ex rx nx
#> <int> <int> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 2000 0 Male 4.26e-3 4.24e-3 1 4.24e-3 0.996 76.0 76.0 0.996 1
#> 2 2000 1 Male 5.93e-4 5.93e-4 0.996 5.90e-4 0.995 75.0 75.3 0.999 1
#> 3 2000 2 Male 2.29e-4 2.29e-4 0.995 2.28e-4 0.995 74.0 74.3 1.000 1
#> 4 2000 3 Male 1.57e-4 1.57e-4 0.995 1.56e-4 0.995 73.0 73.3 1.000 1
#> 5 2000 4 Male 2.21e-4 2.21e-4 0.995 2.20e-4 0.995 72.0 72.3 1.000 1
#> 6 2000 5 Male 1.89e-4 1.89e-4 0.995 1.88e-4 0.994 71.0 71.4 1.000 1
#> 7 2000 6 Male 1.28e-4 1.28e-4 0.994 1.27e-4 0.994 70.0 70.4 1.000 1
#> 8 2000 7 Male 1.27e-4 1.27e-4 0.994 1.26e-4 0.994 69.0 69.4 1.000 1
#> 9 2000 8 Male 9.40e-5 9.40e-5 0.994 9.34e-5 0.994 68.0 68.4 1.000 1
#> 10 2000 9 Male 2.17e-4 2.17e-4 0.994 2.16e-4 0.994 67.0 67.4 1.000 1
#> # ℹ 91 more rows
#> # ℹ 1 more variable: ax <dbl># Life expectancy
norway_mortality |>
filter(Sex != "Total") |>
life_expectancy() |>
ggplot(aes(x = Year, y = ex, color = Sex)) +
geom_line()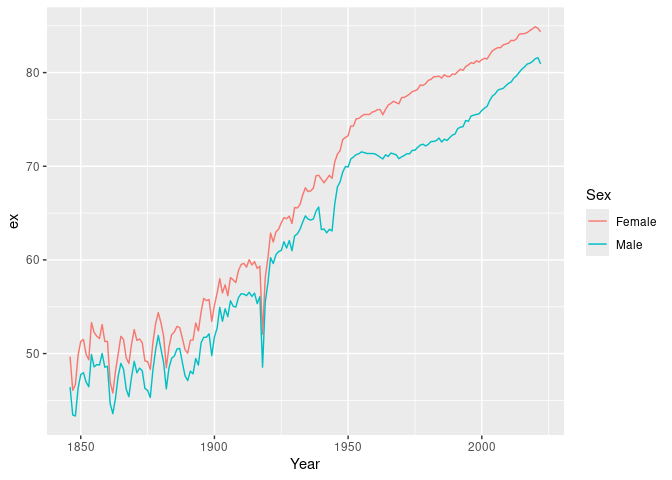
Several smoothing functions are provided:
smooth_spline(), smooth_mortality(),
smooth_fertility(), and smooth_loess(), each
smoothing across the age variable for each year.
# Smoothed data
norway_mortality |>
filter(Sex != "Total", Year == 1967) |>
smooth_mortality(Mortality) |>
autoplot(Mortality) +
geom_line(aes(y = .smooth), col = "#0072B2") +
ylab("Mortality rate") +
scale_y_log10()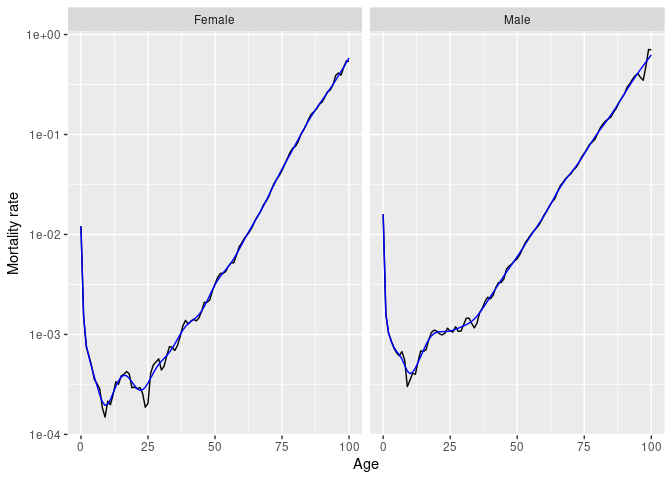
Several mortality models are available including variations on Lee-Carter models (Lee & Carter, JASA, 1992), and functional data models (Hyndman & Ullah, CSDA, 2007).
fit <- norway_mortality |>
filter(Sex != "Total") |>
model(
lee_carter = LC(log(Mortality)),
fdm = FDM(log(Mortality))
)
fit
#> # A mable: 2 x 3
#> # Key: Sex [2]
#> Sex lee_carter fdm
#> <chr> <model> <model>
#> 1 Female <LC> <FDM>
#> 2 Male <LC> <FDM>Models are fitted for all combinations of key variables excluding age.
fit |>
select(lee_carter) |>
filter(Sex == "Female") |>
report()
#> Series: Mortality
#> Model: LC
#> Transformation: log(Mortality)
#>
#> Options:
#> Adjust method: dt
#> Jump choice: fit
#>
#> Age functions
#> # A tibble: 101 × 3
#> Age ax bx
#> <int> <dbl> <dbl>
#> 1 0 -4.33 0.0155
#> 2 1 -6.16 0.0223
#> 3 2 -6.77 0.0193
#> 4 3 -7.14 0.0187
#> 5 4 -7.18 0.0165
#> # ℹ 96 more rows
#>
#> Time coefficients
#> # A tsibble: 124 x 2 [1Y]
#> Year kt
#> <int> <dbl>
#> 1 1900 115.
#> 2 1901 109.
#> 3 1902 103.
#> 4 1903 109.
#> 5 1904 106.
#> # ℹ 119 more rows
#>
#> Time series model: RW w/ drift
#>
#> Variance explained: 66.33%fit |>
select(lee_carter) |>
autoplot()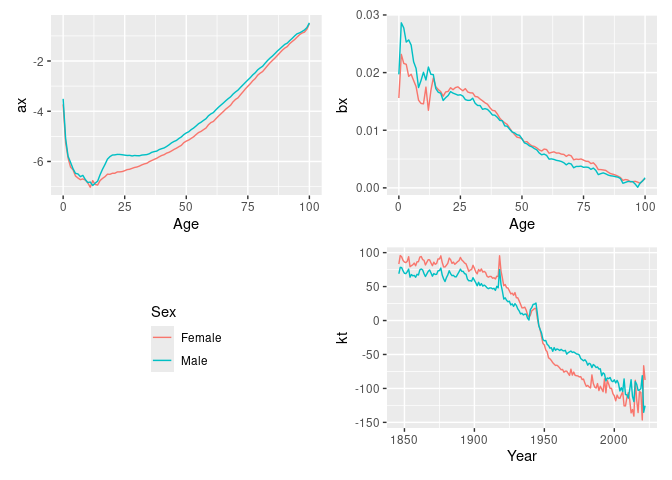
fit |>
select(lee_carter) |>
age_components()
#> # A tibble: 202 × 4
#> Sex Age ax bx
#> <chr> <int> <dbl> <dbl>
#> 1 Female 0 -4.33 0.0155
#> 2 Female 1 -6.16 0.0223
#> 3 Female 2 -6.77 0.0193
#> 4 Female 3 -7.14 0.0187
#> 5 Female 4 -7.18 0.0165
#> 6 Female 5 -7.41 0.0174
#> 7 Female 6 -7.45 0.0165
#> 8 Female 7 -7.48 0.0155
#> 9 Female 8 -7.37 0.0125
#> 10 Female 9 -7.39 0.0124
#> # ℹ 192 more rows
fit |>
select(lee_carter) |>
time_components()
#> # A tsibble: 248 x 3 [1Y]
#> # Key: Sex [2]
#> Sex Year kt
#> <chr> <int> <dbl>
#> 1 Female 1900 115.
#> 2 Female 1901 109.
#> 3 Female 1902 103.
#> 4 Female 1903 109.
#> 5 Female 1904 106.
#> 6 Female 1905 110.
#> 7 Female 1906 101.
#> 8 Female 1907 106.
#> 9 Female 1908 105.
#> 10 Female 1909 99.6
#> # ℹ 238 more rowsfit |> forecast(h = 20)
#> # A vital fable: 8,080 x 6 [1Y]
#> # Key: Age x (Sex, .model) [101 x 4]
#> Sex .model Year Age Mortality .mean
#> <chr> <chr> <dbl> <int> <dist> <dbl>
#> 1 Female lee_carter 2024 0 t(N(-6.8, 0.0088)) 0.00110
#> 2 Female lee_carter 2025 0 t(N(-6.9, 0.018)) 0.00106
#> 3 Female lee_carter 2026 0 t(N(-6.9, 0.027)) 0.00103
#> 4 Female lee_carter 2027 0 t(N(-6.9, 0.036)) 0.00100
#> 5 Female lee_carter 2028 0 t(N(-7, 0.045)) 0.000972
#> 6 Female lee_carter 2029 0 t(N(-7, 0.055)) 0.000944
#> 7 Female lee_carter 2030 0 t(N(-7, 0.064)) 0.000916
#> 8 Female lee_carter 2031 0 t(N(-7.1, 0.074)) 0.000889
#> 9 Female lee_carter 2032 0 t(N(-7.1, 0.084)) 0.000863
#> 10 Female lee_carter 2033 0 t(N(-7.1, 0.094)) 0.000838
#> # ℹ 8,070 more rowsThe forecasts are returned as a distribution column (here transformed
normal because of the log transformation used in the model). The
.mean column gives the point forecasts equal to the mean of
the distribution column.