valytics

Statistical methods for analytical method comparison and validation studies. The package implements Bland-Altman analysis, Passing-Bablok regression, Deming regression, precision experiments, and quality goal specifications based on biological variation — approaches commonly used in clinical laboratory method validation.

Installation

Install valytics from CRAN:

install.packages("valytics")

Or install the development version from GitHub:

# install.packages("pak")
pak::pak("marcellogr/valytics")

Overview

valytics provides tools for analytical method validation:

Method Comparison - Bland-Altman analysis: Assess agreement through bias and limits of agreement - Passing-Bablok regression: Non-parametric regression robust to outliers - Deming regression: Errors-in-variables regression for method comparison

Precision Experiments - Variance component analysis: Repeatability, intermediate precision, reproducibility - Precision verification: Chi-square test against manufacturer claims - Precision profiles: CV vs concentration modeling with functional sensitivity

Quality Specifications - Biological variation-based goals: Calculate allowable total error from CV_I and CV_G - Sigma metrics: Six Sigma quality assessment - Performance assessment: Evaluate methods against quality specifications

All methods produce publication-ready plots and comprehensive statistical summaries.

Method Comparison Examples

Bland-Altman Analysis

library(valytics)

# Compare two creatinine measurement methods
data(creatinine_serum)

ba <- ba_analysis(
  x = creatinine_serum$enzymatic,
  y = creatinine_serum$jaffe
)

ba
#> 
#> Bland-Altman Analysis
#> ---------------------------------------- 
#> n = 80 paired observations
#> 
#> Difference type: Absolute (y - x)
#> Confidence level: 95%
#> 
#> Results:
#>   Bias (mean difference): 0.174
#>     95% CI: [0.127, 0.220]
#>   SD of differences: 0.209
#> 
#> Limits of Agreement:
#>   Lower LoA: -0.236
#>     95% CI: [-0.316, -0.156]
#>   Upper LoA: 0.584
#>     95% CI: [0.504, 0.663]

plot(ba)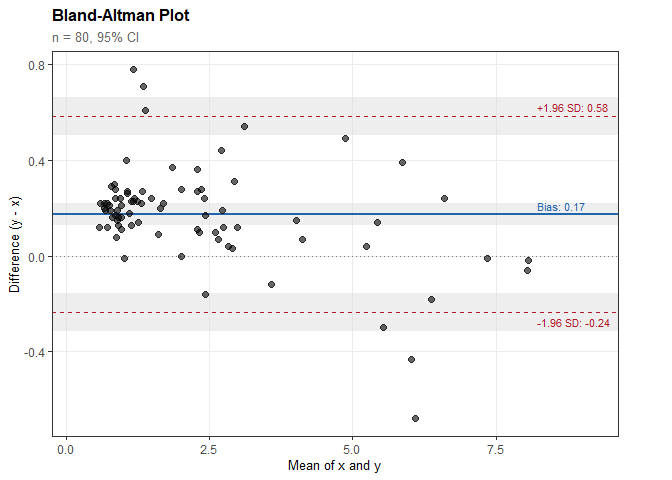

Bland-Altman plot showing differences between Jaffe and enzymatic creatinine methods

Passing-Bablok Regression

pb <- pb_regression(
  x = creatinine_serum$enzymatic,
  y = creatinine_serum$jaffe
)

pb
#> 
#> Passing-Bablok Regression
#> ---------------------------------------- 
#> n = 80 paired observations
#> 
#> CI method: Analytical (Passing-Bablok 1983)
#> Confidence level: 95%
#> 
#> Regression equation:
#>   creatinine_serum$jaffe = 0.234 + 0.971 * creatinine_serum$enzymatic
#> 
#> Results:
#>   Intercept: 0.234
#>     95% CI: [0.229, 0.239]
#>     (excludes 0: significant constant bias)
#> 
#>   Slope: 0.971
#>     95% CI: [0.966, 0.974]
#>     (excludes 1: significant proportional bias)

plot(pb)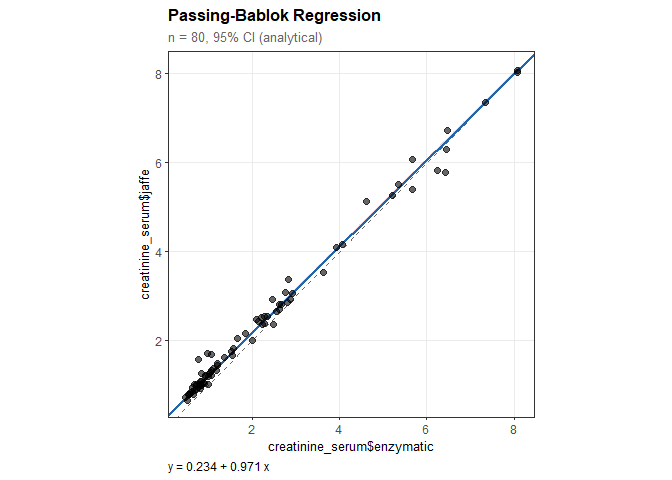

Passing-Bablok regression scatter plot with regression line and confidence band

Deming Regression

dm <- deming_regression(
  x = creatinine_serum$enzymatic,
  y = creatinine_serum$jaffe
)

dm
#> 
#> Deming Regression
#> ---------------------------------------- 
#> n = 80 paired observations
#> 
#> Error ratio (lambda): 1.000
#> CI method: Jackknife
#> Confidence level: 95%
#> 
#> Regression equation:
#>   creatinine_serum$jaffe = 0.277 + 0.953 * creatinine_serum$enzymatic
#> 
#> Results:
#>   Intercept: 0.277 (SE = 0.028)
#>     95% CI: [0.222, 0.332]
#>     (excludes 0: significant constant bias)
#> 
#>   Slope: 0.953 (SE = 0.014)
#>     95% CI: [0.925, 0.982]
#>     (excludes 1: significant proportional bias)

plot(dm)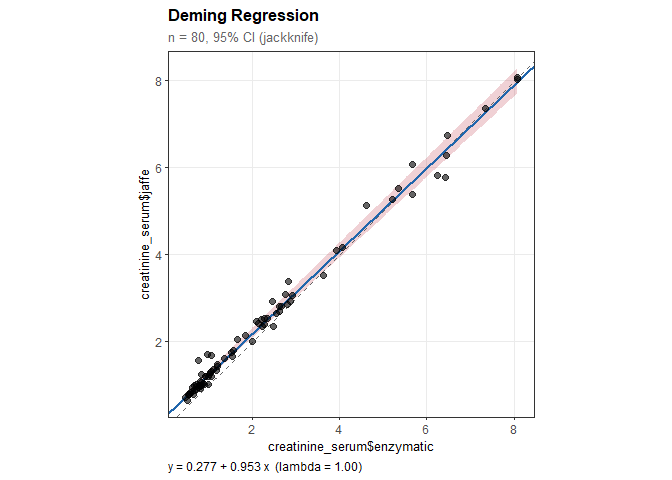

Deming regression scatter plot with regression line and confidence band

Precision Experiments

Variance Component Analysis

# Analyze precision from a multi-day, multi-run study
data(troponin_precision)

prec <- precision_study(
  data = troponin_precision,
  value = "value",
  sample = "level",
  day = "day",
  run = "run"
)

prec
#> 
#> Precision Study Analysis
#> --------------------------------------------- 
#> n = 120 observations
#> Design: day/run/replicate (inferred)
#> Estimation: ANOVA (Method of Moments)
#> CI method: Satterthwaite, 95% CI
#> 
#> Samples: 6 concentration levels
#> (Showing results for first sample; use $by_sample for all)
#> 
#> Precision Estimates:
#> --------------------------------------------- 
#>   Repeatability:       SD = 0.243  (CV = 4.86%)
#>                        95% CI: [0.170, 0.426]
#>   Between-run:         SD = 0.188  (CV = 3.76%)
#>                        95% CI: [0.117, 0.461]
#>   Between-day:         SD = 0.000  (CV = 0.00%)
#>                        95% CI: [0.000, 0.000]
#>   Within-laboratory precision: SD = 0.307  (CV = 6.15%)
#>                        95% CI: [0.227, 0.476]

plot(prec, type = "cv")
#> Warning in data.frame(sample = sample_names[i], mean_conc = if
#> (!is.null(sample_means)) sample_means[sample_names[i]] else i, : Zeilennamen
#> wurden in einer short Variablen gefunden und wurden verworfen

#> Warning in data.frame(sample = sample_names[i], mean_conc = if
#> (!is.null(sample_means)) sample_means[sample_names[i]] else i, : Zeilennamen
#> wurden in einer short Variablen gefunden und wurden verworfen

#> Warning in data.frame(sample = sample_names[i], mean_conc = if
#> (!is.null(sample_means)) sample_means[sample_names[i]] else i, : Zeilennamen
#> wurden in einer short Variablen gefunden und wurden verworfen

#> Warning in data.frame(sample = sample_names[i], mean_conc = if
#> (!is.null(sample_means)) sample_means[sample_names[i]] else i, : Zeilennamen
#> wurden in einer short Variablen gefunden und wurden verworfen

#> Warning in data.frame(sample = sample_names[i], mean_conc = if
#> (!is.null(sample_means)) sample_means[sample_names[i]] else i, : Zeilennamen
#> wurden in einer short Variablen gefunden und wurden verworfen

#> Warning in data.frame(sample = sample_names[i], mean_conc = if
#> (!is.null(sample_means)) sample_means[sample_names[i]] else i, : Zeilennamen
#> wurden in einer short Variablen gefunden und wurden verworfen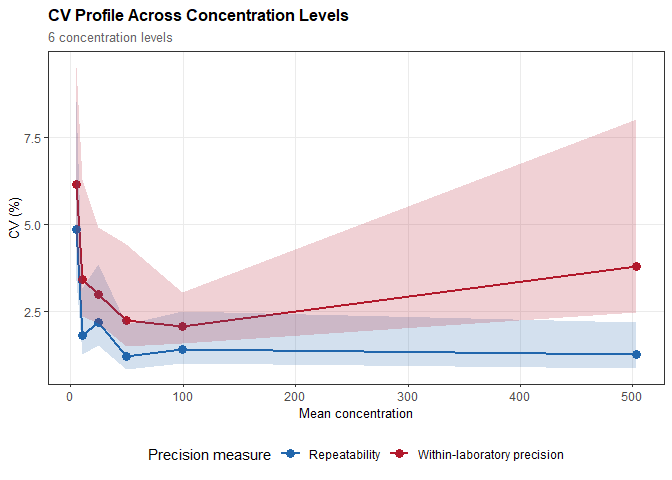

CV profile showing precision measures with confidence intervals

Precision Profiles and Functional Sensitivity

# Model CV vs concentration relationship
prof <- precision_profile(prec, cv_target = 10)

prof
#> 
#> Precision Profile Analysis
#> ---------------------------------------- 
#> n = 6 concentration levels
#> Concentration range: 5 to 503 (100.75-fold)
#> 
#> Model: Hyperbolic
#>   CV = sqrt(2.667^2 + (26.905/x)^2)
#> 
#> Parameters:
#>   a = 2.667
#>   b = 26.905
#> 
#> Fit Quality:
#>   R-squared = 0.816
#>   RMSE = 0.578
#> 
#> Functional Sensitivity:
#>   CV = 10%: concentration = 2.792

plot(prof)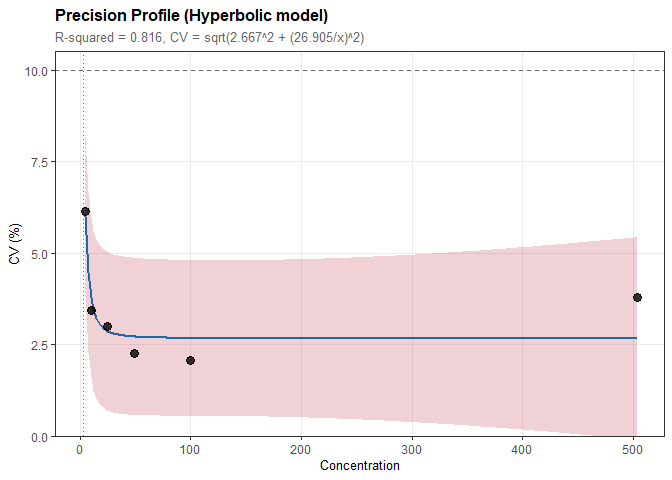

Quality Specifications

Allowable Total Error from Biological Variation

Calculate performance goals based on within-subject (CV_I) and between-subject (CV_G) biological variation:

# Creatinine biological variation (from EFLM database)
# CV_I = 5.95%, CV_G = 14.7%
ate <- ate_from_bv(cvi = 5.95, cvg = 14.7)

ate
#> 
#> Analytical Performance Specifications from Biological Variation
#> ------------------------------------------------------------ 
#> 
#> Input:
#>   Within-subject CV (CV_I): 5.95%
#>   Between-subject CV (CV_G): 14.70%
#>   Performance level: desirable
#>   Coverage factor (k): 1.65
#> 
#> Specifications:
#>   Allowable imprecision (CV_A): 2.98%
#>   Allowable bias: 3.96%
#>   Total allowable error (TEa): 8.87%

Six Sigma Quality Assessment

# Evaluate method performance
sm <- sigma_metric(bias = 1.5, cv = 2.5, tea = 10)

sm
#> 
#> Six Sigma Metric
#> ---------------------------------------- 
#> 
#> Input:
#>   Observed bias: 1.50%
#>   Observed CV: 2.50%
#>   Total allowable error (TEa): 10.00%
#> 
#> Result:
#>   Sigma: 3.40
#>   Performance: Marginal
#>   Defect rate: ~66,800 per million

Performance Assessment

# Full quality assessment
assess <- ate_assessment(
  bias = 1.5, 
  cv = 2.5, 
  tea = 10,
  allowable_bias = 4.0, 
  allowable_cv = 3.0
)

assess
#> 
#> Analytical Performance Assessment
#> -------------------------------------------------- 
#> 
#>   >>> METHOD ACCEPTABLE <<<
#> 
#> Performance Summary:
#>   Parameter              Observed  Allowable     Status
#>   -------------------- ---------- ---------- ----------
#>   Bias                      1.50%      4.00%       PASS
#>   CV (Imprecision)          2.50%      3.00%       PASS
#>   Total Error               5.62%     10.00%       PASS
#> 
#> Sigma Metric: 3.40 (Marginal)

Features

Multiple interfaces: Vector input or formula syntax (method1 ~ method2)
Flexible CI methods: Analytical, Satterthwaite, or bootstrap BCa confidence intervals
Assumption checking: CUSUM linearity test, Shapiro-Wilk normality test
Precision analysis: ANOVA and REML variance component estimation
Quality goals: Biological variation-based specifications (optimal/desirable/minimum)
Publication-ready plots: Built on ggplot2, fully customizable
Tidy workflows: Consistent API, informative summaries

Example Datasets

The package includes four realistic clinical datasets:

Dataset	Description	n
`glucose_methods`	POC meter vs. laboratory analyzer	60
`creatinine_serum`	Enzymatic vs. Jaffe methods	80
`troponin_cardiac`	Two hs-cTnI platforms	50
`troponin_precision`	hs-cTnI precision study (6 levels)	120

Vignettes

Method Comparison Workflow: Step-by-step analysis guide
Understanding Method Comparison Statistics: Educational overview
Deming Regression: When and how to use errors-in-variables regression
Quality Goals from Biological Variation: Setting performance specifications
Precision Profiles and Functional Sensitivity: CV modeling and functional sensitivity

References

Bland-Altman:

Bland JM, Altman DG (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet, 1(8476):307-310.
Bland JM, Altman DG (1999). Measuring agreement in method comparison studies. Statistical Methods in Medical Research, 8(2):135-160.

Passing-Bablok:

Passing H, Bablok W (1983). A new biometrical procedure for testing the equality of measurements from two different analytical methods. Journal of Clinical Chemistry and Clinical Biochemistry, 21(11):709-720.

Deming:

Linnet K (1990). Estimation of the linear relationship between the measurements of two methods with proportional errors. Statistics in Medicine, 9(12):1463-1473.

Precision:

Chesher D (2008). Evaluating assay precision. Clinical Biochemistry Reviews, 29(Suppl 1):S23-S26.
Kroll MH, Emancipator K (1993). A theoretical evaluation of linearity. Clinical Chemistry, 39(3):405-413.

Biological Variation:

Fraser CG, Petersen PH (1993). Desirable standards for laboratory tests if they are to fulfill medical needs. Clinical Chemistry, 39(7):1447-1453.
EFLM Biological Variation Database: https://biologicalvariation.eu/

License

GPL-3

mirror server hosted at Truenetwork, Russian Federation.