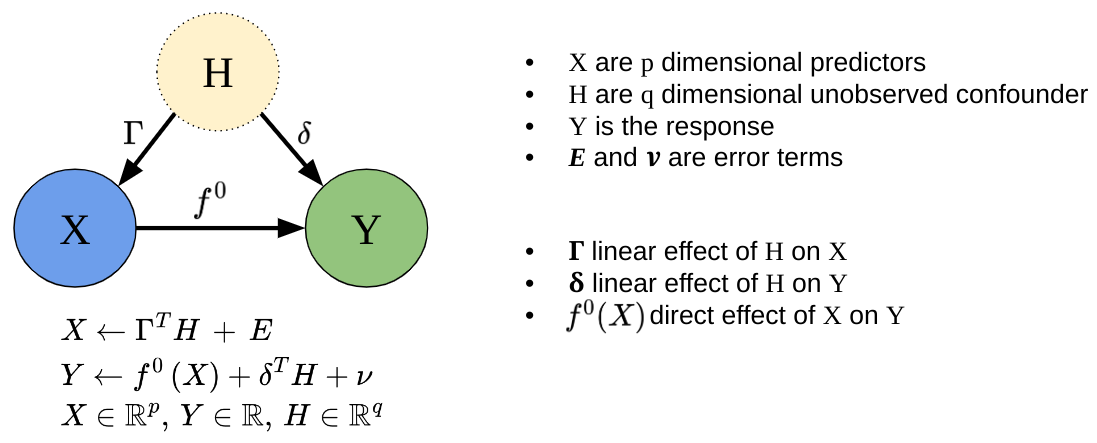
Spectrally Deconfounded Models (SDModels) is a package with methods to screen for and analyze non-linear sparse direct effects in the presence of unobserved confounding using the spectral deconfounding techniques (Ćevid, Bühlmann, and Meinshausen (2020), Guo, Ćevid, and Bühlmann (2022)). These methods have been shown to be a good estimate for the true direct effect if we observe many covariates, e.g., high-dimensional settings, and we have fairly dense confounding. Even if the assumptions are violated, it seems like there is not much to lose, and the SDModels will, in general, estimate a function closer to the true one than classical least squares optimization. SDModels provides software for Spectrally Deconfounded Additive Models (SDAMs) (Scheidegger, Guo, and Bühlmann (2025)) and Spectrally Deconfounded Random Forests (SDForest)(Ulmer, Scheidegger, and Bühlmann (2025)).
To install the SDModels R package from CRAN, just run
install.packages(SDModels)You can install the development version of SDModels from GitHub with:
# install.packages("devtools")
devtools::install_github("markusul/SDModels")or
# install.packages('pak')
# pak::pkg_install('markusul/SDModels')This is a basic example on how to estimate the direct effect of \(X\) on \(Y\) using SDForest. You can learn more about analyzing sparse direct effects estimated by SDForest in the article SDForest.
library(SDModels)
set.seed(42)
# simulation of confounded data
sim_data <- simulate_data_nonlinear(q = 2, p = 50, n = 100, m = 2)
X <- sim_data$X
Y <- sim_data$Y
train_data <- data.frame(X, Y)
# parents
sim_data$j
#> [1] 25 24
fit <- SDForest(Y ~ ., train_data)
fit
#> SDForest result
#>
#> Number of trees: 100
#> Number of covariates: 50
#> OOB loss: 0.17
#> OOB spectral loss: 0.05You can also estimate just one Spectrally Deconfounded Regression
Tree using the SDTree function. See also the article SDTree.
Tree <- SDTree(Y ~ ., train_data, cp = 0.03)
# plot the tree
Tree
#> levelName value s j label decision n_samples
#> 1 1 0.8295434 0.5186858 24 X24 <= 0.52 100
#> 2 ¦--1 0.6418912 -2.0062213 25 X25 <= -2.01 yes 63
#> 3 ¦ ¦--1 0.1522660 NA NA 0.2 yes 9
#> 4 ¦ °--3 0.6609876 NA NA 0.7 no 54
#> 5 °--2 1.1821439 1.5229617 24 X24 <= 1.52 no 37
#> 6 ¦--2 1.0367566 NA NA 1 yes 19
#> 7 °--4 1.4551242 NA NA 1.5 no 18
#plot(Tree)Or you can estimate a Spectrally Deconfounded Additive Model, with
theoretical guarantees, using the SDAM function. See also
the article SDAM.
model <- SDAM(Y ~ ., train_data)
#> [1] "Initial cross-validation"
#> [1] "Second stage cross-validation"
model
#> SDAM result
#>
#> Number of covariates: 50
#> Number of active covariates: 4